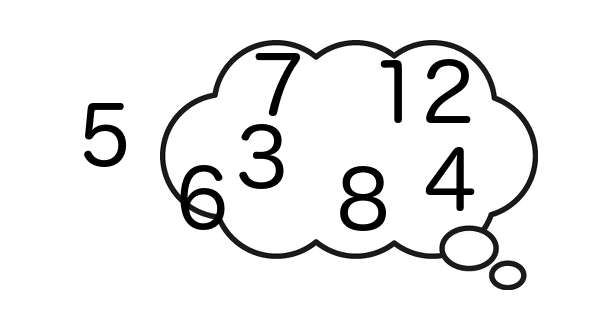ある男の子が「1」から「20」までの整数を全部覚えようとしています。下の条件で覚えるとき、20個すべての数字を覚えるには最短で何日かかるでしょう?
- 最初はどの数字も覚えていない
- 1つの数字を覚えるには1日かかる
- 2のつく数字を覚えるときに、それまでに覚えた数字を覚えた順が古いものから6個忘れる
- 覚えた数字が5個以下のときは、2のつく数字を覚えられない
- 覚えたい20個以外の数字は覚えられない
日能研「シカクいアタマをマルくする。」で出題された問題。相当な難問です。メモリーが少なすぎた時代のコンピューターを思わせる問題です。
日能研で掲載している解答と違う答えがMemCodeでは出ました。私たちが、なにか読み違えている部分があるのかもしれませんが、参考にどうぞ。
- 出典
- 日能研